Imaging & Videochevron_right
Softwarechevron_right
Hardwarechevron_right
linkCarlos Daniel Rincon Mora
linkBio
Tengo 25 años y soy estudiante de Ingeniería de Sistemas y Computación de noveno semestre. Me gusta el desarrollo de Software, especialmente Front End, también el desarrollo de aplicaciones móviles y los videojuegos.
linkInterests
- Desarrollo de aplicaciones móviles
- Desarrollo de videojuegos
- Desarrollo de software
linkContributions
Actualmente no he hecho alguna contribución a ningún proyecto de código abierto, pero me gustaría tener la oportunidad de hacerlo.
linkHobbies
- Ver series y películas
- Crear aplicaciones de juegos
- Practicar varios deportes
- Escuchar e interpretar música
linkIlusion Optica
linkVelo de Alberti
Es una técnica que permite la reducción de escala del natural al dibujo, por medio de una cuadrícula interpuesta formada por hilos gruesos en un tejido de gasa. Fue inventado en el siglo XV por el arquitecto, matemático y filósofo italiano León Battista Alberti. Alberti es considerado el primer teórico artístico del Renacimiento, interesado en la búsqueda de las reglas, tanto teóricas como prácticas, capaces de orientar el trabajo de los artistas. Algunos historiadores como Gisèle Freund, consideran este aparato uno de los principales antecedentes ideológicos de la aparición de la fotografía. Actualmente una técnica parecida se utiliza para pintar telones escenográficos de gran formato, el diseño original habrá sido seccionado con una cuadrícula, permitiéndonos trasladar cada cuadrado en el telón cuadriculado.
linkLeón Battista Alberti
Fue un arquitecto, secretario personal (abreviador apostólico) de tres papas —Eugenio IV, Nicolás V y Pío II—, humanista, tratadista, matemático y poeta italiano. Además de estas actividades principales, también fue criptógrafo, lingüista, filósofo, músico y arqueólogo. Es uno de los humanistas más polifacéticos e importantes del Renacimiento. Alberti fue el primer teórico artístico del Renacimiento, una figura emblemática, por su dedicación a las más variadas disciplinas. Se mostró constantemente interesado por la búsqueda de reglas, tanto teóricas como prácticas, capaces de orientar el trabajo de los artistas; en sus obras menciona algunos cánones. Por ejemplo, en De statua expone las proporciones del cuerpo humano, en De pictura proporciona la primera definición de la perspectiva científica, en De mantua proporciona una definición sobre el reconocimiento especial a las mezclas entre los colores y las formas, especialmente en lo respectivo a los fluidos y sus tipos y por último en De re aedificatoria (obra que termina en 1452) describe toda la casuística relativa a la arquitectura moderna, subrayando la importancia del proyecto, los diversos tipos de edificios siguiendo las funciones que deben desempeñar. El aspecto más innovador de sus propuestas consiste en mezclar lo antiguo y lo moderno propugnando de ese modo la praxis antigua y la moderna, que había iniciado Filippo Brunelleschi. Además, según Alberti: "...el artista en este contexto social no debe ser un simple artesano, sino un intelectual preparado en todas las disciplinas y en todos los terrenos". Una idea heredera del enciclopedismo medieval de los doctos, pero adaptada a la vanguardia humanista. La clase social con la que Alberti se relacionará es la alta burguesía culta florentina. Trabajó al servicio de los mecenas más importantes de su época: el papado, los Este en Ferrara, los Gonzaga en Mantua, los Malatesta en Rímini.
linkMetodologia de uso
Este artilugio permite dibujar con precisión cualquier imagen mediante la ayuda de dos cuadrículas, una situada frente al dibujante y la otra en el papel donde se va a dibujar. Mirando a través de un agujero veremos el objeto a dibujar seccionado en cuadrados, cada uno de los cuales trasladaremos al papel.
Una de las ventajas de esta tecnica es que se puede emplear sin importar el tamaño del retrato, ya que cualquier paisaje se reduce a una cuadricula, y teniendo esta se puede percibir claramente las dimensiones del paisaje completo, sin embargo cuando la imagen a pintar posee muchos detalles, puede volverse un poco tedioso al usar pocos cuadros. Aun asi es un metodo que no ha dejado de usarse hoy en dia, ya que se emplea en muchos lugares sobre todo para los que esta aprendiendo a dibujar.
linkCubrimientos
Es el revestimiento de un plano de dos dimensiones con piezas iguales sin dejar huecos y sin que halla solapamiento.
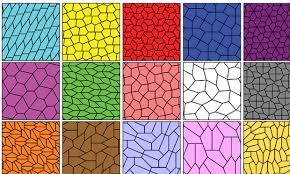
link¿Cual es la forma mas eficaz para cubrir un plano?
Uno de los grandes matematicos griegos, Pappus de Alejandria, dijo en el año 300 que la forma mas eficar de llenar un plano es usando el Hexagono, y se demostro por Thomas Callister Hales en 1999 (Conjetura del Panal de Abeja).
linkPappus de Alejandria
Papo de Alejandría (como epónimo Pappus) (c. 290 – c. 350) fue uno de los últimos grandes matemáticos griegos de la Antigüedad, conocido por su obra Synagoge (c. 340). Apenas se sabe nada de su vida, más que fue maestro en Alejandría y que tuvo un hermano llamado Hermodoro.
Su Synagoge (Colección), es su obra mejor conocida. Es un compendio de matemáticas de ocho volúmenes. Trata de una gran variedad de problemas de geometría, matemática recreativa, duplicado del cubo, polígonos y poliedros.
Pappus vivió en la primera mitad del siglo iv. Su figura sobresale del estancamiento general de la matemática de su época.
En geometría, se le atribuyen varios teoremas, conocidos todos con el nombre genérico de Teorema de Pappus. Entre estos están:
- Teorema del centroide de Pappus,
- La cadena de Pappus,
- Teorema armónico de Pappus
- Teorema del hexágono de Pappus.
linkThomas Callister Hales
Thomas Callister Hales (nacido el 4 de junio de 1958) es un matemático estadounidense que trabaja en las áreas de teoría de la representación, geometría discreta y verificación formal. En teoría de la representación es conocido por su trabajo en el programa Langlands y la prueba del lema fundamental sobre el grupo Sp (4) (muchas de sus ideas fueron incorporadas a la prueba final, debido a Ngô Bảo Châu). En geometría discreta, estableció la conjetura de Kepler sobre la densidad de las empaquetaduras de esferas y la conjetura del panal. En 2014, anunció la finalización del Proyecto Flyspeck, que verificó formalmente la exactitud de su prueba de la conjetura de Kepler.
linkConjetura del Panal de abeja
La conjetura del panal de abeja era una conjetura hasta que se demostró y se convirtió en teorema matemático que afirma que un teselado hexagonal (retícula en forma de panal de abeja) es la mejor manera de dividir una superficie en regiones de igual área y con el mínimo perímetro total.
El primer registro de la conjetura se remonta al 36 aC, de Marco Terencio Varrón, pero a menudo se atribuye a Pappus de Alejandría (c. 290 -. C 350). El teorema fue demostrado en 1999 por el matemático Thomas Callister Hales, quien menciona en su obra que hay razones para creer que la conjetura pueda haber estado presente en la mente de los matemáticos antes de Varrón.
link¿Que pasa cuando no es un plano, sino en tercera dimension?
William Thomson, Lord Kelvin digo que la mejor figura es un octaedro truncado, y pareciera que fuese la mejor figura para cubrir un espacio en tercera dimension, pero nunca llego a demostrarlo.
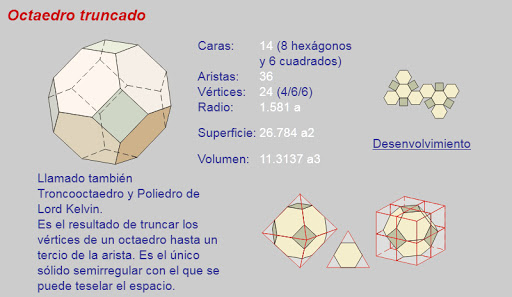
linkWilliam Thomson, Lord Kelvin
William Thomson, Lord Kelvin, (Reino Unido: /ˈwɪlɪəm ˈtɑːmsən lɔːd ˈkelvɪn/; Belfast, Irlanda, 26 de junio de 1824 - Largs, Ayrshire, Escocia, 17 de diciembre de 1907) fue un físico y matemático británico.
Obtuvo los siguientes títulos: Orden de Mérito del Reino Unido, Caballero gran cruz de la Real Orden Victoriana, miembor del Consejo Privado del Reino Unido, Miembro de la Royal Society,creador de la escala de temperatura kevin
Lord Kelvin destacó por sus importantes trabajos en el campo de la termodinámica y la electricidad, gracias a sus profundos conocimientos de análisis matemático. Es uno de los científicos que más contribuyó a modernizar la física. Es especialmente conocido por haber desarrollado la escala de temperatura Kelvin. Recibió el título de barón Kelvin en honor a los logros alcanzados a lo largo de su carrera.
Luego en 1993 dos fisicos, Denis Weaire y Robert Phelan de Trinity College (Dublín), encontraron una mejor figura que el octaedro truncado a la cual llamaron "Estructura de Weaire-Phelan", indagando en un problema de encontrar una estructura de espuma eficaz.
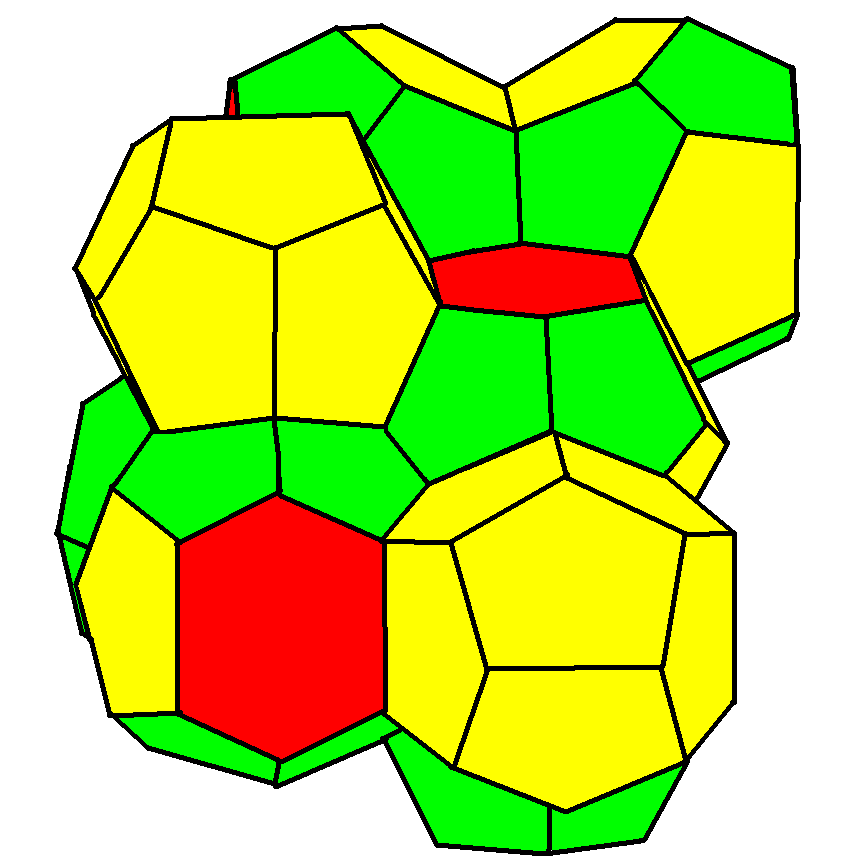
Aun nadie ha encontrado una estructura mejor, ni se ha demostrado que esta se la optima.
Pero aun asi ya tiene un uso, en el edificio de natacion de los juegos olimpicos de Pekin.
linkBibliografia
Carlos Daniel Rincon MoraBioInterestsContributionsHobbiesIlusion OpticaVelo de AlbertiLeón Battista AlbertiMetodologia de usoCubrimientos¿Cual es la forma mas eficaz para cubrir un plano?Pappus de AlejandriaThomas Callister HalesConjetura del Panal de abeja¿Que pasa cuando no es un plano, sino en tercera dimension?William Thomson, Lord KelvinBibliografia